\( \)

arduino

hardware

Arduino C语法

详细可以参考已有文件

数据类型

  • boolean 布尔
  • char 字符类型
  • byte 字节类型
  • int 整数类型
  • unsigned int 无符号整型
  • long 长整型
  • unsigned long 无符号长整型
  • float 实数类型
  • double
  • string
  • array
  • void

常量

HIGH / LOW 表示数字IO的电平 INPUT / OUTPUT 表示数字IO口的方向，INPUT表示输入，OUTPUT表示输出 true/ false 表示真假

结构

void setup() 初始化发量，管脚模式，调用库函数 void loop() 连续执行函数内的语句

功能

数字IO

  • pinMode(pin, mode) 输入输出IO口模式定义函数，pin表示为0~13，mode表示INPUT或者OUTPUT
  • digitalWrite(pin, value) 数字IO口输出电平定义函数，pin表示0~13，value表示为HIGH或者LOW
  • int digitalRead(pin) shuziio口读取输入电平函数，pin表示0~13返回值表示高电平或者低电平HIGH or LOW

模拟IO

  • int analogRead(pin)_ 模拟io口读函数，pin表示0~5(根据硬件的接口来定)
  • analogWrite(pin, value)_PWM 数字io口PWM输出函数，arduino数字io口标注了PWM的IO口可使用该函数，pin表示3，5，6，9，10，11，value表示0~255

时间函数

  • delay(ms) 延时函数，单位ms
  • delayMicroseconds(us) 延时函数，单位us

数学函数

  • min(x, y) 求最小值
  • max(x, y) 求最大值
  • abs(x) 计算绝对值
  • constrain(x, a, b) 约束函数，下限a， 上限b， x必须在ab之间才能返回
  • map(value, fromLow, fromHigh, toLow, toHigh) 约束函数，value必须在范围值之间
  • pow(base, exponent) 开方函数，base的exponent次方
  • sq(x) 平方
  • sqrt(x) 开平方

ADXL335

3自由度加速度计量传感器

ADXL335三轴加速计的使用案例

根据加速度求取倾角的原理(官方)
官方网站针对加速计的使用进行了详细说明

参考地址CSDN
使用加速计进行读取数据的案例

官方网址
对ADXL335型号加速计详细的介绍，包括硬件部分

根据加速度求取倾角的具体计算过程：

百度上的参考

2示意图

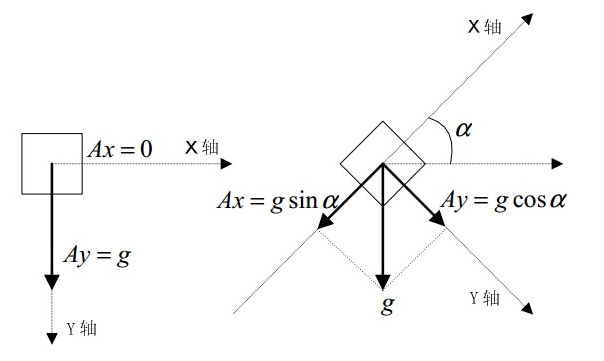
如图所示，有 \(A_x = g \sin \alpha\), \(A_y = g \cos \alpha\), then \(\frac{A_x}{A_y} = \tan \alpha\), 即 \(\alpha = \arctan( \frac{A_x}{A_y} )\)
这样，就可以根据在x、y轴上的加速度求取倾斜角度

注意：这是静止状态，运动过程需要提高采样频率

二维平面具有局限性，所以使用3维的加速度计算

与上面类似的计算过程，可以得出倾斜角度公式 \(\alpha = \arctan \frac {\sqrt{ A_x^2 + A_z^2 }}{A_y}\)

因为双\{\{问题导致语法编译错误, 暂时使用原始公式表达式

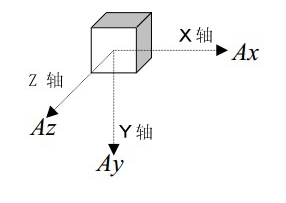
3维示意图

x需要说明的是，这里利用的是物体静止时受到重力的性质，如果物体同时也有加速度的话，这个公式不再准确, 需要增加一个限制条件

\[\begin {cases} \alpha = \arctan(\frac{\sqrt { A_x^2 + A_y^2 }}{A_y}) \\ \sqrt{ A_x^2 + A_z^2 + A_y^2 } = 1g \end{cases}\]

软件算法

如上公式所示的计算方法
反三角函数算法

  1. 测量xyz三轴的加速度，Ax、Ay、Az
  2. 计算\(A_x^2 + A_z^2 + A_y^2\)，如果这个平方接近1g的平方，那么说明这组采样值是有效的，可以用来计算，否则丢弃，重复第一步
  3. 利用有效的采样值，通过开平方和反正切函数的科学计算，计算出倾斜角度\(alpha = \arctan(\frac{\sqrt{A_x^2+A_z^2}}{A_y})\)
  4. 重复第一步

查表算法

第一种算法的计算两庞大，需要高性能硬件的配合。如果避开这些计算，则可以大幅度降低算法复杂度
分两步降低算法复杂度：

  1. 利用整数开方代替C函数开方
  2. 利用查表代替正切计算，即提前计算每个角度\(\alpha\)的正切值\(\tan\)，并保存在EEPROM中，那么在计算过程中，只需要计算\(\frac{\sqrt{A_x^2 + A_z^2}}{A_y}\)，并在表中查找接近的正切值，那么相应的角度就是所求角度

倾斜角度的精度与角速度的分辨率之间的额关系

根据前面的计算公式，又有\(\sqrt{A_x^2+A_y^2+A_z^2} = 1g\)可以简化公式为\(\alpha = \arctan(\frac{\sqrt{(1g)^2 - A_y^2}}{A_y})\), 公式中只有一个变量Ay

倾斜角度越大，精度越低，具体参考前面的百度网址